「数の不思議」

執筆:金蘭千里中学校・高等学校 数学科 井藤 吉紀
こんにちは。小学校で日々、算数の授業を楽しんでいますか。数と遊んでいますか。今日は、数の不思議について少しだけお話ししていきたいと思います。
みなさんは、美しい「完全数(かんぜんすう)」を知っていますか。小説「博士の愛した数式」を読んで、知った人もいるかもしれません。まずは少し、算数のおさらいをしておきます。
「2つの整数 ○, △ について、○=△×(整数) とかけるとき、△は○の約数(○は△の倍数)という。 例として、 6 = 3 ×2 なので、3は6の約数である。(6の約数は、1, 2, 3, 6 である。)」
では、「完全数」とは、ある整数でその数自身を除いたすべての約数の和(足し算)がもとの数と等しくなる数である。
例として、
6 = 1 + 2 + 3 , 28 = 1 + 2 + 4 + 7 + 14 (神秘的ですネ。)
よって、「6, 28」は完全数である。
他にも、「496, 8128」などがあります。
次に数を増やしていきます。「友愛数(ゆうあいすう)」とは、2つの整数のうち、一方の数のその数自身を除いたすべての約数の和が他方の数自身と互いに等しくなるような一組の数である。親和数(しんわすう)とも呼ばれています。
例として、
220 → 1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284
284 → 1 + 2 + 4 + 71 + 142 = 220
(面白い関係ですネ。)
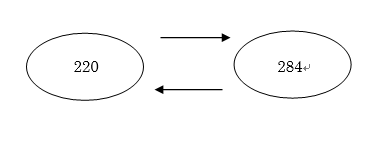
よって、「220と284」は、友愛数である。
他にも探してみてはどうでしょう。「1184と1210」などがあります。 友愛数は2つの整数のお話でしたが、3つ以上のお話もあります。
最後に「社交数(しゃこうすう)」とは、ある整数 (A) のその数自身を除いた約数の和が他の数 (B) になり、(B) のその数自身を除いた約数の和が (C) になる。これを続けていくと、もとの数 (A) になるような3つ以上の数の組である。
例として、
12496 → 1+2+4+8+11+16+22+44+71+88+142+176+284+568+781+1136+1562+3124+6248=14288
14288 → 1+2+4+8+16+19+38+47+76+94+152+188+304+376+752+893+1786+3572+7144=15472
15472 → 1+2+4+8+16+967+1934+3868+7736=14536
14536 → 1+2+4+8+23+46+79+92+158+184+316+632+1817+3634+7268=14264
14264 → 1+2+4+8+1783+3566+7132=12496
(計算が大変ですけど、発見の喜びがありますネ。)
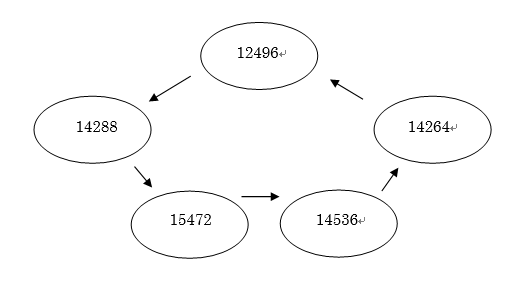
よって、「12496と14288と15472と14536と14264」は社交数である。
みなさんも友人と仲良く手を取り合って、協力して学校生活を楽しんで下さい。
数の美しさ、神秘性、不思議な数の世界を少しだけのぞいてもらいました。理科と同じように実験してみると、様々な発見があります。これからも数と遊びながら、「なぜだろう」という気持ちを大切に算数を楽しんでいってください。
進学教室浜学園























