【中学受験】有名中学現役教諭の”数学”特別授業～正多角形を拡張して考える～
有名中の授業は、好奇心をくすぐる仕掛けが盛りだくさん。そして、学ぶことの本質を突いた授業は、探求心あふれる生徒を育てます。さあ、あなたも知的な冒険に出かけましょう！
正多角形を拡張して考える
執筆：北嶺中・高等学校 教諭 数学科 藤元 貴之
自然に隠された多角形
みなさんこんにちは。4月に入り、ここ北嶺中学校のある北海道もあたたかくなり、雪も解け、昆虫たちも動き出しています。本州では桜が咲いているようですが、北海道は5月上旬が見ごろになりそうです。実はこのような自然の植物や昆虫には君たちが良く知っている図形が隠されています。例えば、雪の結晶や虫の複眼などは必ず六角形になっています。また、桜の花びらは必ず5つで等間隔に開いており、星形五角形のような形になっています。今回はこのような多角形について、数を拡張して考えていこうと思います。
もっと読む
正2.5角形とは？
正三角形、正四角形（正方形）、正五角形といえば、どのような形かは容易に想像できるでしょう。君たちは整数のほかに小数や分数を習っていると思います。そこで、今回は正2.5角形（正5/2角形）とはどのような図形になるか考えてみましょう。
正多角形について
さて、正2.5角形について考えるにあたって、まずは正多角形とは、どのようなものなのか確認しましょう。「正多角形（正n角形）とは、n個の辺の長さが等しく、n個の内角の大きさが等しい多角形である。基本的に、nは３以上の整数とする。」
この文章に基づくと、n=2.5について考えるのは難しいです。
他の視点から正多角形の性質について考えてみましょう。例えば内角について考えてみると、正三角形の一つの内角は60°、正四角形（正方形）は90°、正五角形は108°、正n角形の一つの内角は{180×(n-2)÷n}°となります。 なぜこうなるかは君たちであれば理解できるでしょうから省略します。このように、正多角形の内角に注目すると
「正多角形（正n角形）とは、すべての辺の長さが等しく、一つの内角が{180×(n-2)÷n}°の多角形である。」・・・★
と、考えることができます。
正2.5角形＝星形五角形？
★で考えると、正2.5角形は、一つの内角が{180×(2.5-2)÷2.5}°、つまりは「すべての辺の長さが等しく、一つの内角が36°の多角形」となります。さあ、定規と分度器を出して、書いてみてください。下記のようになったでしょう。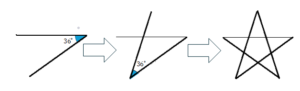
なんと、正2.5角形は星形5角形になるということが分かります。
さまざまな正多角形
もちろん、2.5角形以外の小数・分数についてもnが2以上であれば、★の考え方で図形を描くことができます。以下にいくつか紹介します。（77.14度） 正3.50角形 ７辺
（8.57度） 正2.10角形 21辺
さて正多角形について、小数・分数についても考えることができると分かり、数を拡げて考えることの面白さが分かったと思います。さらに、上記の図形に関して、分数表記の分母、分子（正三角形等は正3/1角形と考えます）、頂点の数、繋いでいる点の間隔等について考えてみるとまた新しい性質を発見できるはずです。ここでは、どのような性質が見つかるかは書かないので、自分でたくさん考えてみてください。
