西大和学園中学校が贈る算数コラム④ Eureka(エウレカ)!

執筆:奈良県北葛城郡 西大和学園中学校 数学科
西大和学園中学校が贈る算数コラム④Eureka(エウレカ)!
*ギリシャ語に由来する感嘆詞、何かを発見・発明したことを喜ぶときに使われる。古代ギリシアの数学者・発明者であるアルキメデスが叫んだとされる言葉。
『半径が1の円の面積を求めなさい。』
と問われたら、皆さんは、何の疑いもなくA=πr^2という公式に数値を当てはめて、簡単に円の面積を求めてしまう事でしょう。円周率πは約3.14なので、半径と半径と円周率をかけ合わせ、円の面積は約3.14と答えるはずです。この、“当たり前感覚”の具体的手順は算数や数学の問題を解いていく緊張感漂う入試の時や試験の時には非常に役立ちます。しかしなぜ、この公式が成り立つかを考える暇は入試や試験の時にはありません。
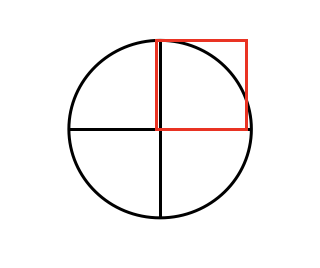
この円の半径が1であれば、正方形の1辺の長さは1ですから、その面積は1です。また、円の面積はこの正方形の3倍以上であることが確認できます。それは、半径がいくらであっても、円の面積は、四分円を含む正方形の3倍以上であることが確認できます。それは約3.14で、A=πr^2という式から半径がいくらの円であっても円の面積は四分円を含む正方形のπ倍であることを表しています。
この事実だけでもA=πr^2が、『円の面積を正しく求めるための具体的手順』の役割を果たしているだけではないという事がわかります。
次に、πr2 は πr×r とも書けます。これは、縦が r 、横がπr の長方形の面積とみなすことができます。 ギリシャの大数学者アルキメデスは、次のようなことに気がつきました。
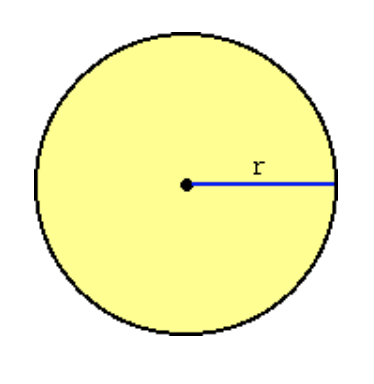
を、
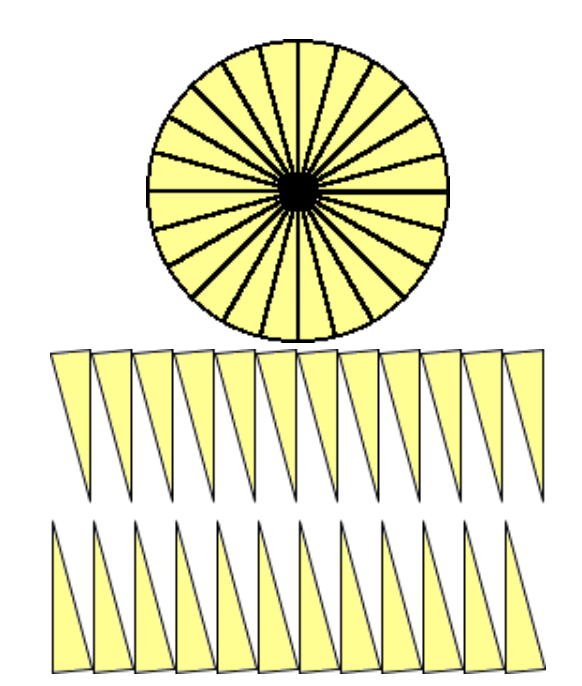
という具合に多くの小さな薄片に分けて、小さな長方形のような形に並べ変えます。
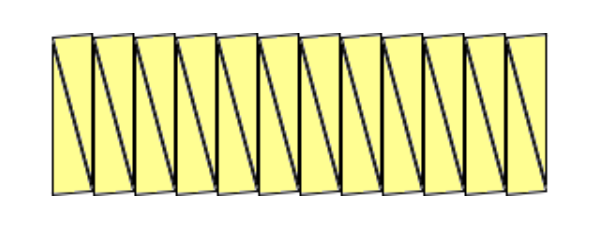
薄片がもっと多くなれば、その一つ一つは三角形に近い形になり、並べ変えられたものは長方形に近づいていきます。 この長方形の縦の長さは r (これは円の半径)、横の長さは円の周囲の半分(直径×円周率の半分)πr です。 したがって、この長方形の面積は、r×πr すなわち πr2 となります。
一つの式 πr2 が多くの方法で解釈しなおすことができるというのは、非常に有益で説得力のあるものです。 しかし、一つひとつの表現は、ほんのわずかな情報しか伝えていません。3つ目の長方形の話も、円の周囲の長さがナゼ、2πrになるのか説明されていませんし、薄片を並べ替えたものを強引に長方形と言い切っているのも“気持ち悪さ”が残りますよね。
この気持ち悪さを追求することや、一つの式を、まるで文学作品のように味わうことも数学の魅力の一つでもあり、皆さんが中学校や高等学校に進学したときに出会う数学の世界なのです。なんだかワクワクしてきませんか?
進学教室浜学園
西大和学園中学校が贈る算数コラム④Eureka(エウレカ)!
*ギリシャ語に由来する感嘆詞、何かを発見・発明したことを喜ぶときに使われる。古代ギリシアの数学者・発明者であるアルキメデスが叫んだとされる言葉。
『半径が1の円の面積を求めなさい。』
と問われたら、皆さんは、何の疑いもなくA=πr^2という公式に数値を当てはめて、簡単に円の面積を求めてしまう事でしょう。円周率πは約3.14なので、半径と半径と円周率をかけ合わせ、円の面積は約3.14と答えるはずです。この、“当たり前感覚”の具体的手順は算数や数学の問題を解いていく緊張感漂う入試の時や試験の時には非常に役立ちます。しかしなぜ、この公式が成り立つかを考える暇は入試や試験の時にはありません。

この円の半径が1であれば、正方形の1辺の長さは1ですから、その面積は1です。また、円の面積はこの正方形の3倍以上であることが確認できます。それは、半径がいくらであっても、円の面積は、四分円を含む正方形の3倍以上であることが確認できます。それは約3.14で、A=πr^2という式から半径がいくらの円であっても円の面積は四分円を含む正方形のπ倍であることを表しています。
この事実だけでもA=πr^2が、『円の面積を正しく求めるための具体的手順』の役割を果たしているだけではないという事がわかります。
次に、πr2 は πr×r とも書けます。これは、縦が r 、横がπr の長方形の面積とみなすことができます。 ギリシャの大数学者アルキメデスは、次のようなことに気がつきました。

を、

という具合に多くの小さな薄片に分けて、小さな長方形のような形に並べ変えます。

薄片がもっと多くなれば、その一つ一つは三角形に近い形になり、並べ変えられたものは長方形に近づいていきます。 この長方形の縦の長さは r (これは円の半径)、横の長さは円の周囲の半分(直径×円周率の半分)πr です。 したがって、この長方形の面積は、r×πr すなわち πr2 となります。
一つの式 πr2 が多くの方法で解釈しなおすことができるというのは、非常に有益で説得力のあるものです。 しかし、一つひとつの表現は、ほんのわずかな情報しか伝えていません。3つ目の長方形の話も、円の周囲の長さがナゼ、2πrになるのか説明されていませんし、薄片を並べ替えたものを強引に長方形と言い切っているのも“気持ち悪さ”が残りますよね。
この気持ち悪さを追求することや、一つの式を、まるで文学作品のように味わうことも数学の魅力の一つでもあり、皆さんが中学校や高等学校に進学したときに出会う数学の世界なのです。なんだかワクワクしてきませんか?
進学教室浜学園























