算数で広がる世界

執筆:北海道札幌市 北嶺中・高等学校 数学科教諭 荻原悦夫
かつて北嶺中学の入試でも扱われた「ピタゴラス音階」を理解するには、小学校で学習する分数が分かれば十分です。ピタゴラスは古代ギリシャの人で、中学校で習う「ピタゴラス(三平方)の定理」にも名前が出てきます。
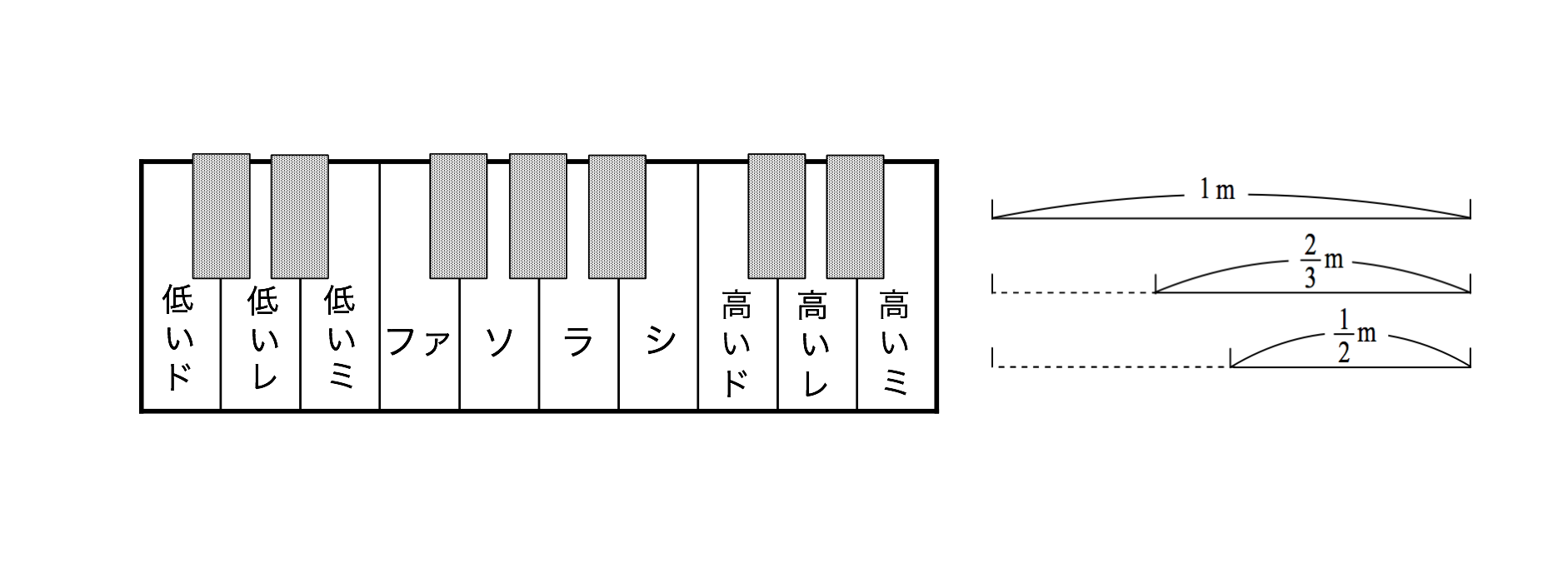
仮に、1メートルの長さの弦で低いドの音が出たとすると、2分の1の長さにしてはじくと(1オクターブ)高いドの音が、3分の2の長さにしてはじくと(完全5度高い)ソの音がそれぞれ出ます。ピタゴラスは、このことに着目して音階を構成したと言われています。
完全5度高い音は、白い鍵盤も黒い鍵盤も含めて数えて7番目にあたる音です。例えば、図の鍵盤で、低いドの音に対してソの音、ソの音に対して高いレの音、低いレの音に対してラの音、ラの音に対して高いミの音が、それぞれ完全5度高い音になります。このことを利用して、低いドの音を出す弦の長さを基準1として、他の音を出す弦の長さを決めていきます。まず、ソの音は3分の2、高いレの音は、完全5度高いのでさらに3分の2倍して9分の4、低いレの音は、1オクターブ低いので2倍して9分の8というように構成します。これを続けて、ラの音は27分の16、高いミの音は81分の32、低いミの音は81分の64、・・・・・・という具合です。
この辺までくると、分数も簡単でなくなってきます。分数を使う音階の仕組みには、「純正律」というのもあって、低いミの音は5分の4を対応させます。(簡単な分数のほうが、ドと響きがよく調和するのです。)
音階の仕組みは、いくつもありますが、現在よく使われる「平均律」というのは、中学・高校で「無理数」を習うと理解することができます。算数(数学)の学習が進むにつれ、理解できる世界が広がるのも楽しみの一つです。
進学教室浜学園
かつて北嶺中学の入試でも扱われた「ピタゴラス音階」を理解するには、小学校で学習する分数が分かれば十分です。ピタゴラスは古代ギリシャの人で、中学校で習う「ピタゴラス(三平方)の定理」にも名前が出てきます。

仮に、1メートルの長さの弦で低いドの音が出たとすると、2分の1の長さにしてはじくと(1オクターブ)高いドの音が、3分の2の長さにしてはじくと(完全5度高い)ソの音がそれぞれ出ます。ピタゴラスは、このことに着目して音階を構成したと言われています。
完全5度高い音は、白い鍵盤も黒い鍵盤も含めて数えて7番目にあたる音です。例えば、図の鍵盤で、低いドの音に対してソの音、ソの音に対して高いレの音、低いレの音に対してラの音、ラの音に対して高いミの音が、それぞれ完全5度高い音になります。このことを利用して、低いドの音を出す弦の長さを基準1として、他の音を出す弦の長さを決めていきます。まず、ソの音は3分の2、高いレの音は、完全5度高いのでさらに3分の2倍して9分の4、低いレの音は、1オクターブ低いので2倍して9分の8というように構成します。これを続けて、ラの音は27分の16、高いミの音は81分の32、低いミの音は81分の64、・・・・・・という具合です。
この辺までくると、分数も簡単でなくなってきます。分数を使う音階の仕組みには、「純正律」というのもあって、低いミの音は5分の4を対応させます。(簡単な分数のほうが、ドと響きがよく調和するのです。)
音階の仕組みは、いくつもありますが、現在よく使われる「平均律」というのは、中学・高校で「無理数」を習うと理解することができます。算数(数学)の学習が進むにつれ、理解できる世界が広がるのも楽しみの一つです。
進学教室浜学園























